
Belgisiz sayılar için hangi örnekler verilebilir?
Belgisiz sayılar, belirli bir miktar veya değer belirtmeyen, belirsiz durumları ifade eden kavramlardır. Matematikte ve günlük yaşamda sıkça karşılaşılan bu terimler, belirsizlik ve değişkenlik içeren durumları tanımlamak için kullanılır. Örneklerle bu kavramın kullanım alanları açıklanmıştır.
Belgisiz Sayılar ve Tanımları Belgisiz sayılar, genellikle belirli bir miktar veya değer belirtmeyen, belirsiz veya tanımsız olan sayılardır. Matematikte ve günlük yaşamda sıkça karşılaşılan bu kavram, değişkenlik ve belirsizlik içeren durumları ifade etmek için kullanılır. Belgisiz sayılar, genellikle soyut matematiksel kavramlar ya da somut olaylar üzerinde yapılan tanımlamalarda karşımıza çıkar. Belgisiz Sayı Örnekleri Belgisiz sayılar çeşitli alanlarda kullanıldığından, aşağıda bu bağlamda bazı örnekler verilmiştir:
Belgisiz Sayıların Matematiksel Kullanımı Matematiksel bağlamda belgisiz sayılar, özellikle değişkenlerin kullanıldığı durumlarda ortaya çıkar. Örneğin, bir denklemde "x" veya "y" gibi harfler, belirli bir sayıyı temsil etmeyen belgisiz sayılardır. Bu tür ifadeler, aşağıdaki durumlarda kullanılabilir:
Gündelik Hayatta Belgisiz Sayılar Gündelik yaşamda belgisiz sayılar, iletişimde sıkça kullanılan ifadelerdir. İnsanlar, kesin bir sayı vermek yerine belirsizlik içeren ifadeleri tercih edebilirler. Bu bağlamda, belgisiz sayılar aşağıdaki durumlarda kullanılır:
Sonuç Belgisiz sayılar, matematik ve gündelik yaşamda önemli bir yer tutar. Bu tür ifadeler, belirsizliği ve değişkenliği ifade etmek amacıyla kullanılır. Örnekler üzerinden incelendiğinde, belgisiz sayıların ne kadar yaygın ve çeşitli olduğu görülmektedir. Bu nedenle, belgisiz sayılar hem matematiksel alanlarda hem de günlük iletişimde önemli bir rol oynamaktadır. Ekstra Bilgiler Belgisiz sayılar, aynı zamanda sosyal bilimler, ekonomi ve istatistik gibi alanlarda da sıkça kullanılır. Özellikle belirsizlik ve risk analizi konularında, belgisiz sayıların uygun bir şekilde ifade edilmesi, karar verme sürecinde kritik bir öneme sahiptir. Bu bağlamda, belgisiz sayıların tanımlanması ve kullanılması, daha sağlıklı bir analiz ve değerlendirme süreci sağlar. |




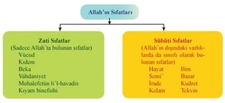

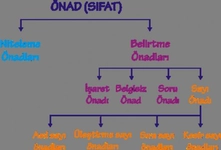

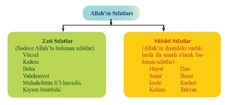






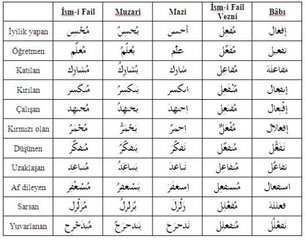
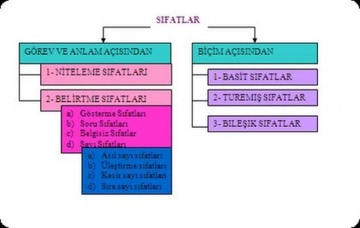
















Bu içerik gerçekten de belgisiz sayıların matematikte ve günlük yaşamda ne kadar yaygın ve önemli olduğunu çok iyi özetliyor. Birkaç kişi ifadesinin yanı sıra, yaklaşık fiyatlar ya da belirsiz zaman dilimleri gibi örnekler oldukça gerçekçi ve günlük hayatta sıkça karşılaştığımız durumları yansıtıyor. Sizce de belgisiz sayılar, belirsizlik içeren durumları ifade ederken insan iletişiminde bir köprü görevi görmüyor mu? Özellikle sosyal bilimler ve ekonomi gibi alanlarda belgisiz sayılar kullanılarak yapılan analizlerin karar verme süreçlerindeki etkisi hakkında ne düşünüyorsunuz?
Belgisiz Sayıların Önemi
Özengin, belgisiz sayılar gerçekten de matematikte ve günlük hayatta önemli bir yere sahiptir. Belirsizlik içeren durumları ifade etmemiz gerektiğinde, bu tür sayılar iletişimde köprü vazifesi görür. Özellikle sosyal bilimler ve ekonomi gibi alanlarda, belgisiz sayılar kullanarak yapılan analizler, belirsizlikleri daha iyi anlamamıza ve karar verme süreçlerimizi yönlendirmemize yardımcı olur.
İletişimdeki Rolü
Belgisiz sayılar, kesin olmayan durumları tanımlarken insanların birbirleriyle daha etkili bir şekilde iletişim kurmasına olanak tanır. Örneğin, "yaklaşık 100 kişi" ifadesi, kesin bir sayı vermektense, durumu daha anlaşılır hale getirir. Bu tür ifadeler, iletişimde belirsizliği azaltma ve daha net bir anlayış sağlama amacı taşır.
Karar Verme Süreçleri
Sosyal bilimler ve ekonomi gibi alanlarda belgisiz sayıların kullanımı, analizlerin doğruluğunu artırabilir. Bu sayılar, tahminlerde bulunmamıza ve gelecekteki olasılıkları değerlendirmemize olanak tanır. Örneğin, bir ekonomik modelde belirsiz sayılar kullanarak, pazarın ne yönde ilerleyebileceğini daha iyi kestirebiliriz. Dolayısıyla, belgisiz sayılar, karar verme süreçlerinde önemli bir rol oynamaktadır ve bu durum, daha bilinçli seçimler yapmamıza yardımcı olur.