
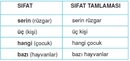
Asıl sayılar sıfatları nasıl tanımlar?
Asıl sayılar, matematiğin temel yapı taşlarından biridir. Bu yazıda, asıl sayıların tanımı ve özellikleri ele alınacak, matematiksel bağlamda önemine vurgu yapılacaktır. Asıl sayıların pozitif, tam ve sonsuz olma nitelikleri, matematiksel işlemlerdeki rolünü belirlemektedir.
Asıl Sayılar Sıfatları Nasıl Tanımlar?Asıl sayılar, matematikte önemli bir kavramdır ve sıfatları, bu sayıların belirli özelliklerini tanımlamak için kullanılır. Bu makalede, asıl sayıların tanımları, sıfatları ve bu sıfatların matematiksel bağlamdaki önemi üzerinde durulacaktır. Asıl Sayıların Tanımı Asıl sayılar, 1, 2, 3, 4,... şeklinde devam eden pozitif tam sayılardır. Bu sayılar, doğal sayılar kümesinin bir alt kümesi olup, matematiksel işlemler ve sayı teorisi açısından büyük bir öneme sahiptir. Asıl sayıların en temel özellikleri şunlardır:
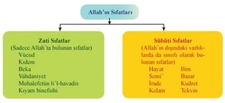
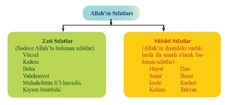
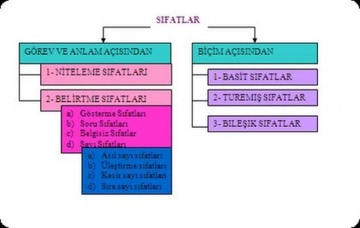
Asıl Sayıların Sıfatları Asıl sayıların sıfatları, bu sayıların özelliklerini ve niteliklerini tanımlamak için kullanılır. Bu sıfatlar genellikle aşağıdaki gibidir:
Asıl Sayıların Matematikteki Önemi Asıl sayılar, matematikte birçok alanda kritik bir rol oynamaktadır. Bu sayıların önemi, aşağıdaki başlıklar altında incelenebilir:
Sonuç Asıl sayılar, matematiğin temel taşlarını oluşturan önemli bir sayı kümesidir. Sıfatları, bu sayıların özelliklerini tanımlamakta ve matematiksel işlemlerdeki yerini belirlemektedir. Matematiksel teoriler ve uygulamalar açısından asıl sayıların rolü, onların pozitif, tam, sonsuz ve birinci olma nitelikleri ile doğrudan ilişkilidir. Bu nedenle, asıl sayıların sıfatlarını ve tanımlarını anlamak, matematiksel düşüncenin gelişimi için kritik bir adımdır. |




























Asıl sayılar hakkında daha fazla bilgi edinmek istiyorum. Bu sayıları tanımlarken kullanılan sıfatların, matematiksel işlemlerde nasıl bir rol oynadığını merak ediyorum. Özellikle pozitif ve tam olma özellikleri, günlük hayatta nasıl bir anlam taşıyor? Ayrıca, asal sayıların sonsuz sayıda olması matematiksel teorilere nasıl katkıda bulunuyor? Bu konular üzerinde biraz daha derinleşebilir miyiz?
Asal Sayılar Nedir?
Asal sayılar, yalnızca 1 ve kendisi olmak üzere tam iki pozitif böleni olan doğal sayılardır. Yani, asal sayılar 1 ve kendisi dışında hiçbir tam sayıya bölünemez. Örneğin, 2, 3, 5, 7, 11 gibi sayılar asal sayılardır.
Matematiksel İşlemlerde Kullanılan Sıfatlar
Asal sayılar tanımlanırken kullanılan "pozitif" ve "tam" sıfatları, bu sayıları diğer sayılardan ayıran önemli özelliklerdir. "Pozitif" ifadesi, sayının sıfırdan büyük olduğunu belirtirken, "tam" ifadesi ise kesirli veya ondalıklı olmamasını ifade eder. Bu özellikler, asal sayıların matematiksel işlemler içinde nasıl kullanılacağını belirler. Örneğin, asal sayıların çarpanları yalnızca kendisi ve 1 olduğundan, bu sayılar faktörizasyon ve sayı teorisi gibi alanlarda önemli bir rol oynar.
Günlük Hayatta Asal Sayıların Anlamı
Günlük hayatta asal sayılar, şifreleme sistemleri, veri güvenliği ve algoritmalar gibi birçok alanda kullanılır. Özellikle bilgisayar bilimlerinde, asal sayılar, veri şifrelemede ve güvenli iletişimde temel bir yapı taşıdır.
Asal Sayıların Sonsuzluğu ve Matematiksel Teorilere Katkısı
Asal sayıların sonsuz sayıda olduğunu kanıtlayan Öklid'in teoremi, matematiğin temel taşlarından biridir. Bu durum, sayı teorisi ve matematiksel analiz gibi alanlarda birçok yeni teorinin geliştirilmesine yol açmıştır. Asal sayıların dağılımı üzerine yapılan çalışmalar, matematiksel modellemelerde önemli veriler sunar ve bu da farklı alanlarda uygulama bulur.
Sonuç olarak, asal sayılar hem matematiksel teorilerin temelini oluşturur hem de pratik uygulamalarda önemli bir yere sahiptir. Bu nedenle, asal sayılar hakkında daha fazla bilgi edinmek, matematiksel düşüncenizi ve problem çözme yeteneklerinizi geliştirmenize yardımcı olabilir.