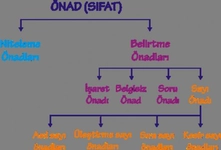
Asıl sayı sıfatı nedir, örnekleri nelerdir?

Asıl sayılar, matematikte etkileyici bir yer tutan ve birçok alanda önemli uygulamaları bulunan bir kavramdır. Bu makalede, asıl sayının ne olduğu, özellikleri ve örnekleri üzerinde durulacaktır.

Asıl Sayı Tanımı

Asıl sayılar, doğal sayıların bir alt kümesidir ve genellikle "doğal sayılar" olarak bilinen 1, 2, 3, 4,... gibi sayılardır. Bu sayılar, sayma işlemlerinde kullanılır ve negatif sayıların, kesirli sayıların ya da ondalık sayıların dışında kalan pozitif tam sayılardır.

Asıl Sayıların Özellikleri

Asıl sayıların bazı temel özellikleri şunlardır:

• Asıl sayılar her zaman pozitif tam sayılardır.
• Asıl sayılar, sıfırdan başlayarak sonsuza kadar devam eder.
• Asıl sayılar, toplama ve çarpma işlemlerine tabidir; yani iki asıl sayının toplamı veya çarpımı her zaman bir asıl sayıdır.
• Asıl sayılar, doğal sayıların alt kümesi olup, doğal sayılar arasında yer alır.

Asıl Sayıların Kullanım Alanları

Asıl sayılar, çeşitli alanlarda yaygın olarak kullanılmaktadır. İşte bazı örnekler:

• Matematiksel işlemlerde sayma ve ölçme işlemleri için kullanılır.
• Bilgisayar bilimlerinde, algoritmaların karmaşıklığını ölçmek için kullanılır.
• İstatistiksel analizlerde, veri setlerinin büyüklüğünü ifade etmek için kullanılır.
• Ekonomi ve finans alanında, borç miktarları ve gelir hesaplamaları için kullanılır.

Asıl Sayılara Örnekler

Asıl sayılara örnek vermek gerekirse:

• 1
• 2
• 3
• 10
• 100

Bu örnekler, asıl sayıların tanımına uygun olarak sıralanmıştır.

Sonuç

Asıl sayılar, matematiksel temellerin oluşturulmasında önemli bir role sahiptir. Sayma, ölçme ve çeşitli matematiksel işlemler için vazgeçilmez bir araçtır. Asıl sayıların özellikleri ve kullanım alanları, onların matematikteki önemini vurgular. Bu nedenle, asıl sayılar, hem teorik hem de pratik açıdan büyük bir öneme sahiptir.

Ekstra Bilgiler

Asıl sayılar, matematiksel kavramların ötesinde, günlük yaşamda da sıkça karşılaştığımız bir unsurdur. Örneğin, alışverişlerde fiyatların belirlenmesinde, yaş hesaplamalarında ve zaman yönetiminde asıl sayılara sıkça ihtiyaç duyulmaktadır. Ayrıca, matematiksel oyunlar ve bulmacalarda da asıl sayılar önemli bir yer tutmaktadır.Asıl sayıların daha ileri düzeydeki matematiksel kavramları, sayı teorisi gibi alanlarda incelenmektedir ve bu sayılar, daha karmaşık yapıların temellerini oluşturur. Bu bağlamda, asıl sayılar sadece temel matematikte değil, aynı zamanda ileri düzey matematiksel çalışmaların da önemli bir parçasıdır.