
Beşinci Sayının Sıfatı Nedir?
Beşinci sayının sıfatı, matematiksel ve dilbilgisel açıdan önemli bir kavramdır. Bu yazıda, beşinci sayının tanımı, sıfat kavramının önemi ve kullanım alanları detaylandırılacaktır. Beşinci sayının özellikleri, sayılar arası ilişkilerin anlaşılmasına katkı sağlar.
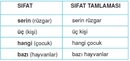
Beşinci sayının sıfatı, matematiksel ve dilbilgisel bir kavram olarak, belirli bir sayı ile ilişkili olan nitelikleri ifade eder. Bu makalede, beşinci sayının sıfatlarının tanımı, önemi ve kullanım alanları üzerinde durulacaktır. Beşinci Sayının Tanımı Beşinci sayı, doğal sayıların sıralı dizisinde 5. pozisyonda yer alan bir sayıdır. Doğal sayılar, 0'dan başlayarak pozitif tam sayıları içerdiğinden, beşinci sayının değeri 5'tir. Beş, matematiksel işlemlerde, sayısal analizlerde ve çeşitli uygulamalarda önemli bir yere sahiptir. Sıfat Kavramı ve Önemi Sıfat, bir ismin özelliklerini veya durumunu belirten bir dilbilgisi terimidir. Beşinci sayının sıfatı, bu sayıyı tanımlayan veya nitelendiren bir ifadedir. Sıfatlar, sayılara, nesnelere veya kavramlara belirli özellikler kazandırarak onları daha anlamlı hale getirir. Beşinci sayının sıfatı, "beşinci" kelimesi ile ifade edilir ve bu sıfat, sıralama, konum veya sıralı bir dizinin parçası olma özelliğini belirtir. Beşinci Sayının Sıfatı Kullanım Alanları Beşinci sayının sıfatı, çeşitli alanlarda ve bağlamlarda kullanılabilir. Bu bağlamlar arasında şunlar bulunmaktadır:
Sonuç Beşinci sayının sıfatı, matematiksel ve dilbilgisel açıdan önemli bir kavramdır. Bu sıfat, sayının konumunu ve sıralı bir dizinin parçası olma özelliğini belirtir. Beşinci sayının sıfatı, çeşitli alanlarda ve uygulamalarda kullanılarak, sayılar arasındaki ilişkiyi anlamamıza yardımcı olur. Beşinci sayının sıfatı, hem akademik çalışmalarda hem de günlük hayatta karşımıza çıkan bir kavramdır ve bu sayede sayılarla ilgili daha derin bir anlayış geliştirmemize olanak tanır. Ekstra Bilgiler Beşinci sayının sıfatı, özellikle matematiksel formüller ve işlemler açısından büyük bir öneme sahiptir. Örneğin, beşinci terimi bulmak için kullanılan formüller, dizilerin ve serilerin analizinde kritik bir rol oynamaktadır. Ayrıca, beşinci sayının sıfatı, çeşitli bilim dallarında, özellikle de sosyal bilimlerde, veri analizinde ve sıralama sistemlerinde sıkça kullanılmaktadır. Bu nedenle, beşinci sayının sıfatı, hem teorik hem de pratik alanlarda önemini korumaktadır. |




























Beşinci sayının sıfatı hakkında düşündüğümde, bu kavramın matematiksel ve dilbilgisel açıdan ne kadar önemli olduğunu fark ediyorum. Beşinci sayının sıfatı olan beşinci kelimesi, gerçekten de sayının konumunu ve sıralı bir dizideki yerini net bir şekilde ifade ediyor. Bu durum, özellikle matematiksel hesaplamalarda ve istatistikte, verilerin analizinde büyük bir rol oynuyor. Sıfatların, bir nesnenin ya da kavramın özelliklerini belirttiğini düşündüğümüzde, beşinci sayının sıfatının günlük hayatta da nasıl kullanıldığını merak ediyorum. Acaba, bu kavramı daha iyi anlamak için günlük yaşamda karşılaştığımız örneklerden hangileri bizim için daha öğretici olabilir?
Beşinci Sayının Sıfatı ve Önemi
Saçı, beşinci sayının sıfatı üzerine düşüncelerin oldukça yerinde. Matematiksel ve dilbilgisel açıdan bu kavramın önemi gerçekten büyük. Beşinci kelimesi, yalnızca bir sayının sırasını belirtmekle kalmaz, aynı zamanda o sayının konumunu ve ilişkisini de net bir şekilde ortaya koyar. Özellikle istatistiksel veriler ve analizlerde, sıralama ve konum belirleme kritik bir rol oynar.
Günlük Hayatta Kullanımı
Günlük yaşamda, beşinci sayının sıfatını kullanabileceğimiz birçok örnek bulunuyor. Örneğin, bir yarışmada katılımcıların sıralanması sırasında "beşinci" ifadesi, kimin hangi pozisyonda olduğunu anlamak için önemlidir. Ayrıca, bir etkinlikteki beşinci konuşmacıdan bahsettiğimizde, bu kişinin konumunun ve öneminin altını çizeriz.
Öğretici Örnekler
Öğretici olabilecek bir diğer örnek ise, kitapların sıralanmasında veya müzik albümlerinin listelenmesinde "beşinci" ifadesinin nasıl kullanıldığıdır. Bu tür örnekler, sıfatların günlük hayatta nasıl işlev gördüğünü ve matematiksel düşüncenin dilbilgisiyle nasıl birleştiğini anlamamıza yardımcı olabilir. Bu sayede, yalnızca sayılarla değil, aynı zamanda kelimelerle de düşünmeyi öğrenmiş oluruz.